HOME技術情報TECHNICAL KNOWLEDGEBASE（【Grating Package】 ）ユーザー定義メリット関数による高NA ビームスプリッターの最適化

TECHNICAL KNOWLEDGEBASE

2023-02-15

【Grating Package】

ユーザー定義メリット関数による高NA ビームスプリッターの最適化

ファイルをダウンロード

回折ビームスプリッターは、位相と構造、その逆が直接的に関係するため、しばしば近軸近似を適用して設計されています。非近軸または高NA スプリッターの場合、これらの近似はある程度の不正確さをもたらすので、追加の厳密なポスト最適化ではないにしても、少なくとも厳密な解析が推奨されます。この事例では、奇数次の回折光を使用した典型的なバイナリ構造の1: 6 スプリッターを例にとり、厳密な評価を実施します。このために、初期光学系の構造をパラメータ化し、一連のユーザー定義メリット関数をProgrammable Grating Analyzer を介して定義します。パラメトリック最適化とその後の公差解析には、厳密なフーリエモーダル法（FMM）を使用します。

モデリング概要

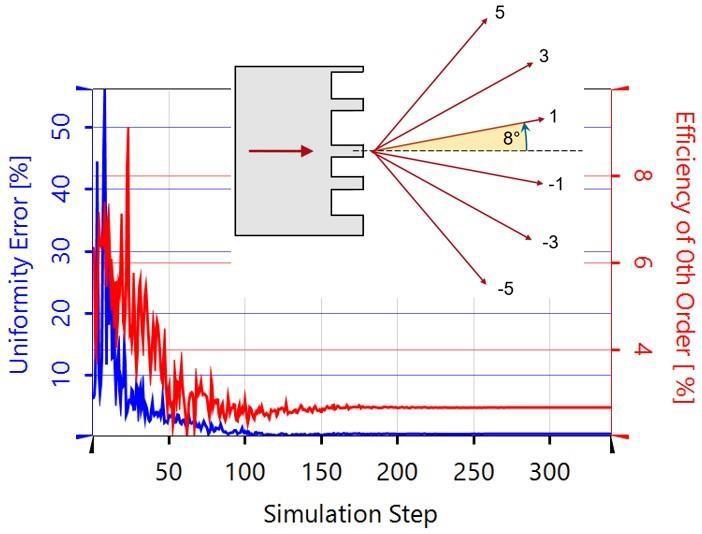
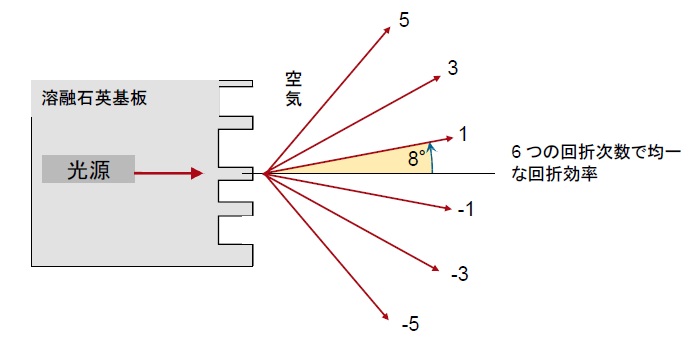
以下の回折型高NA 1: 6 ビームスプリッターの表面形状を最適化し、所望の次数で最適な均一性を達成するにはどうすればよいでしょうか。

光源パラメータ

  • 波長: 632.63 nm
  • 偏光: x 軸偏光

回折ビームスプリッター面

  • ARコーティングのないバイナリ面
  • 周期: 4.545 μm
  • 最小構造サイズ: 431nm

回折ビームスプリッター面の初期設計(*)

  1. 初期ビームスプリッターの位相関数はVirtualLab Fusion の反復フーリエ変換アルゴリズム（IFTA）設計ツールで計算しました。
  2. 高さプロファイルへの変換には、Thin Element Approximation（TEA）に基づくStructure Design を適用しました。

(*)この事例には含まれません　(**)これらのセッションエディタは、Diffractive Optics Toolbox Silver で使用できます。

TEAと等距離サンプリング構造の制限

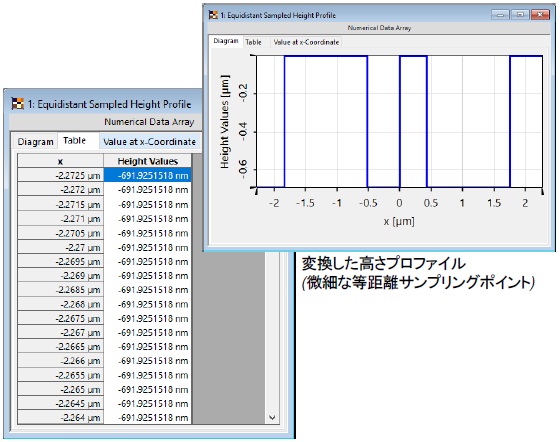
  • 最小の構造サイズが波長の～5 倍より小さくない場合は、TEA がよく適しています。これがそうでない場合、設計された高さプロファイルと相互作用した後の振幅 位相分布は、望ましい値からずれを示す可能性があります。
  • したがって、厳密な評価が必要です。
  • また、パラメトリック最適化の場合は、構造データを別の方法で定義する必要があります。

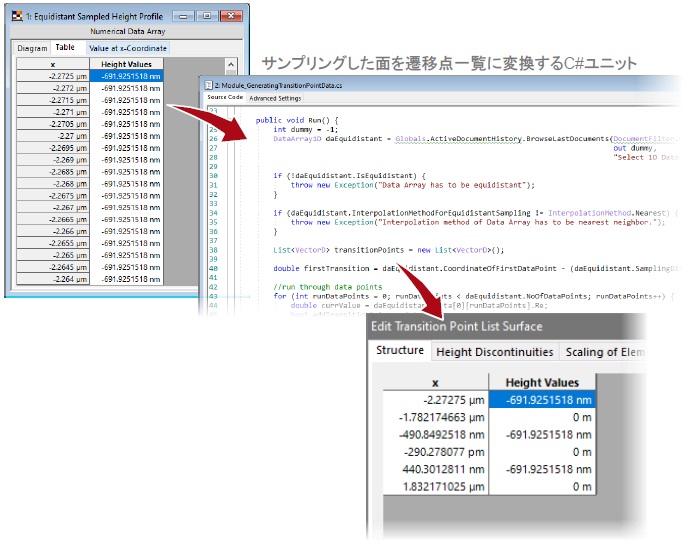
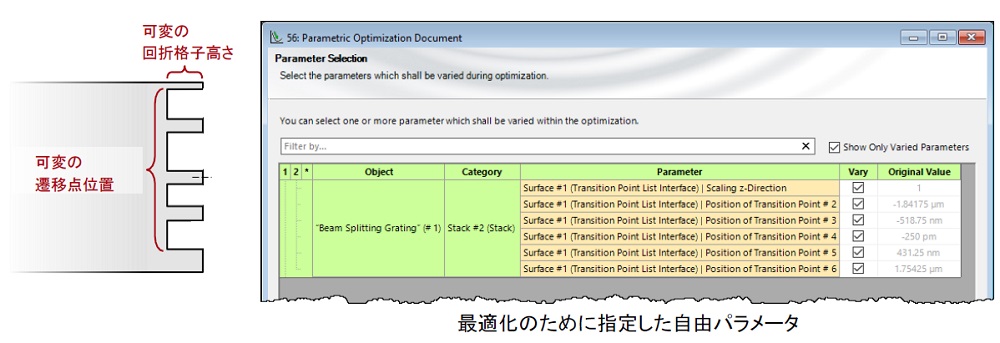
ポスト最適化のためのデータ準備（パラメータ化）

  • フーリエモーダル法（FMM）での厳密解析には、structure design 機能でサンプリングされた高さプロファイルをそのまま使用できます。
  • ただし、パラメトリック最適化の場合は、一連のパラメータを使用できるように、構造をパラメータ化する必要があります。
  • このために、等距離サンプリングされた表面データを非等距離遷移点リストに変換するVirtualLab Fusion モジュールを使用します（添付のサンプルファイルに含まれます）。

さらなる最適化のための回折ビームスプリッター面

パラメトリック最適化のために使用するのは以下のとおりです:

  • 遷移点の位置(*)
  • およびフリーパラメーターとしてとしてのz-scaling factor（すなわち、プロファイルの高さ）

(*)素子の境界を定義する最初の点を除きます。

どの回折次数でどのメリット関数を使用しますか？

最適化のためには、単にパラメーター化された構造だけでなく、回折次数の結果に基づいて計算される適切なメリット関数を定義することも重要です。

この事例では、以下のメリット関数を定義します:

  1. 所望（動作）次数の効率
  2. 所望（動作）次数の均一性誤差
  3. 不要次数の最大効率（0 次光を除く）
  4. 不要な0 次光の効率
  5. 不要次数の効率

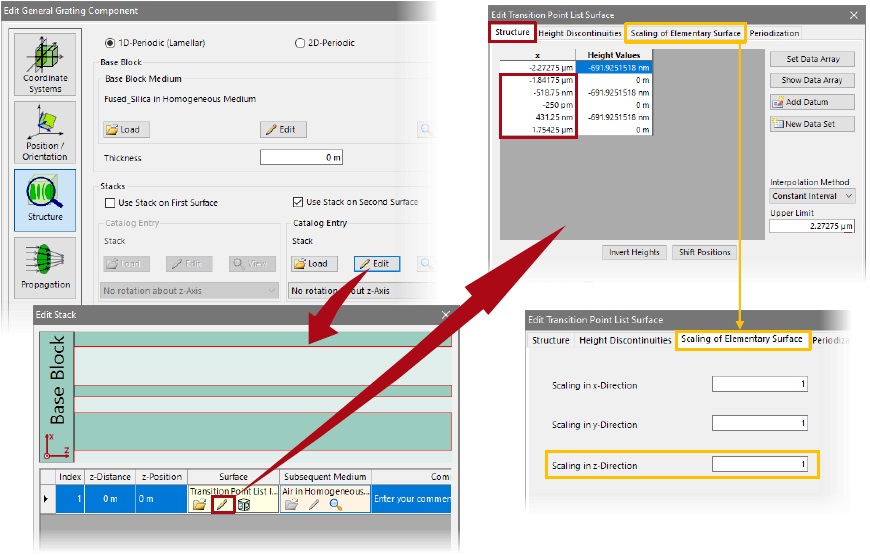
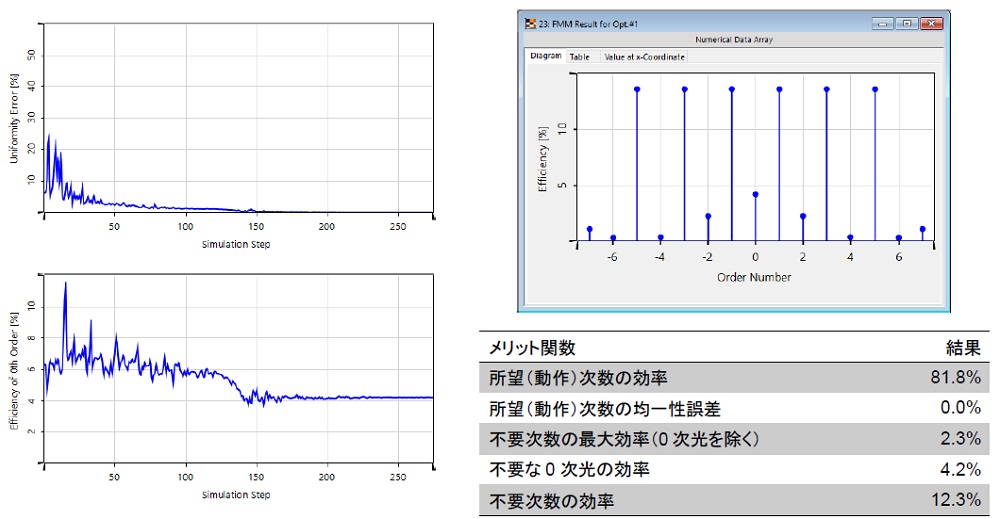
6つの所望の（動作）次数は、-5 、-3 、-1 、1 、3 、5 で、いくつの不要な次数を考慮すべきでしょうか？
→伝搬次数の数を確かめるためにVirtualLab Fusion のDiffraction Angle Calculator を用いました。

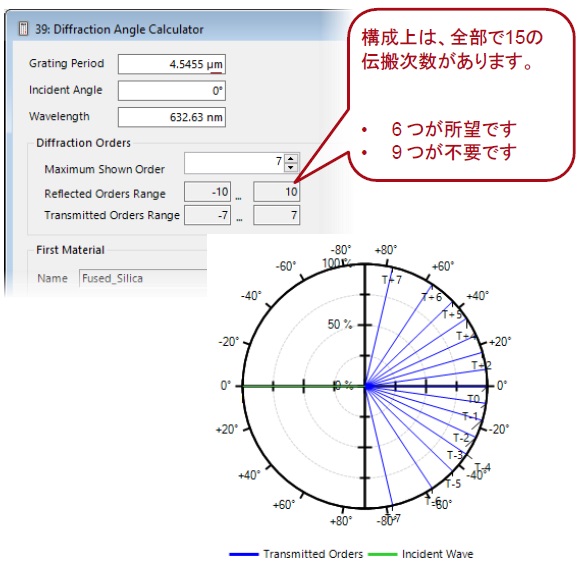
Programmable Grating Analyzer の使用

組み込みのGrating Order Analyzer は、対象となるすべての効率を多様な方法で表示できる優れたツールです。

しかし、任意に所望のメリット関数を定義するには、Programmable Grating Analyzer が最適なツールです。

初期設計のビームスプリッターの厳密な解析

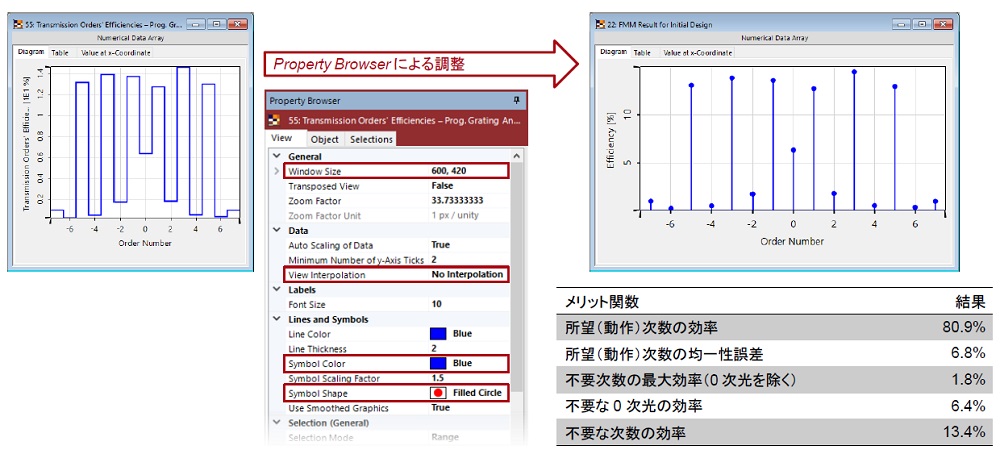
最適化パラメータの設定

比較のための二つの最適化プロセス

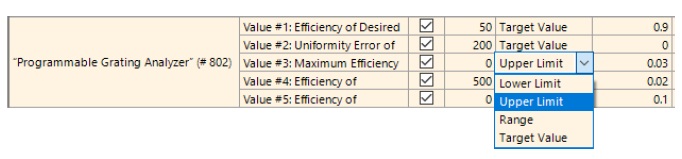
この事例では、目標と制約の設定が異なる2 つの最適化を示します：

  • 最適化#1 では、均一性誤差を優先します。
  • 最適化#2 では、0 次光も同様に最小化する必要があります。

メリット関数の制約について、ユーザーは以下を指定できます。

  • 個々の目標値、範囲、下限値または上限値と
  • それらの寄与度を重みで指定します。

この最適化には組み込みのDown Hill Simplex アルゴリズムを適用します。

メリット関数の制約の構成

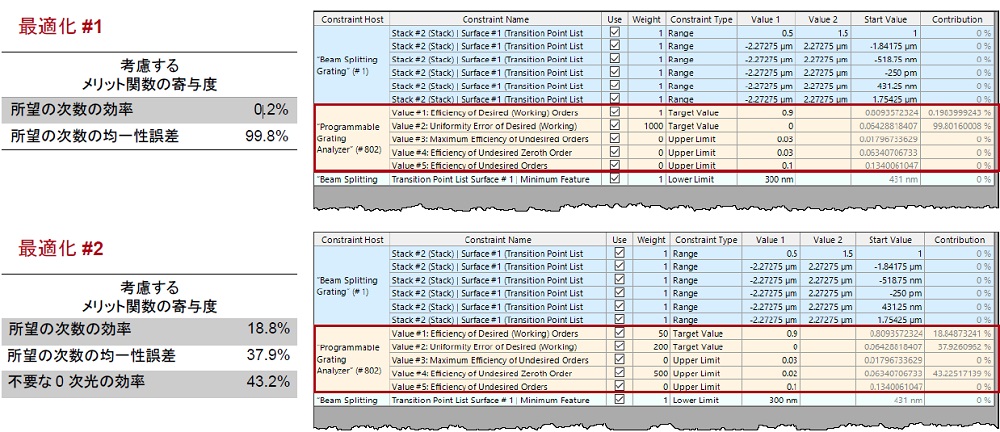
最適化 #1（優先項目 = 均一性誤差）

最適化 #2（優先項目 = 均一性誤差と低い0 次光）

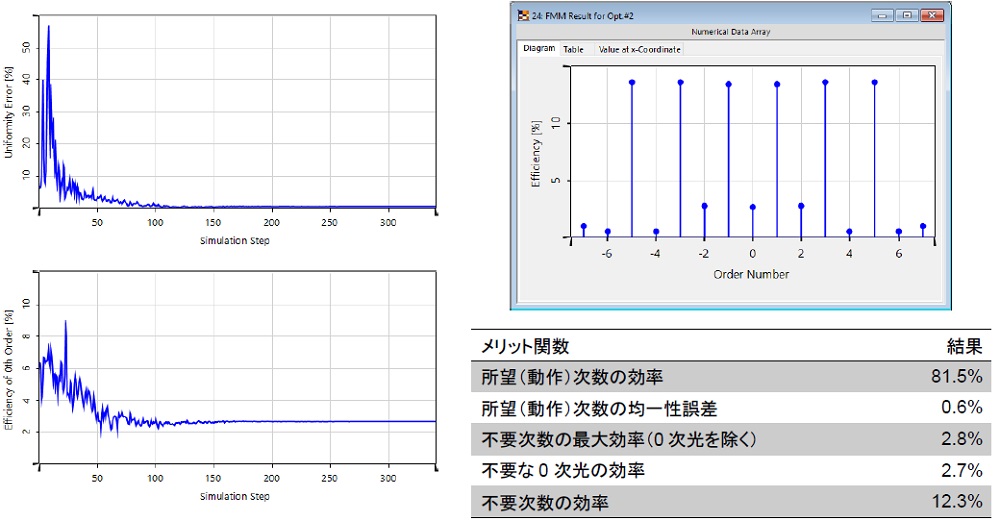
厳密な結果の比較（初期 - 最適化 #1 - 最適化 #2）

公差シミュレーションの結果

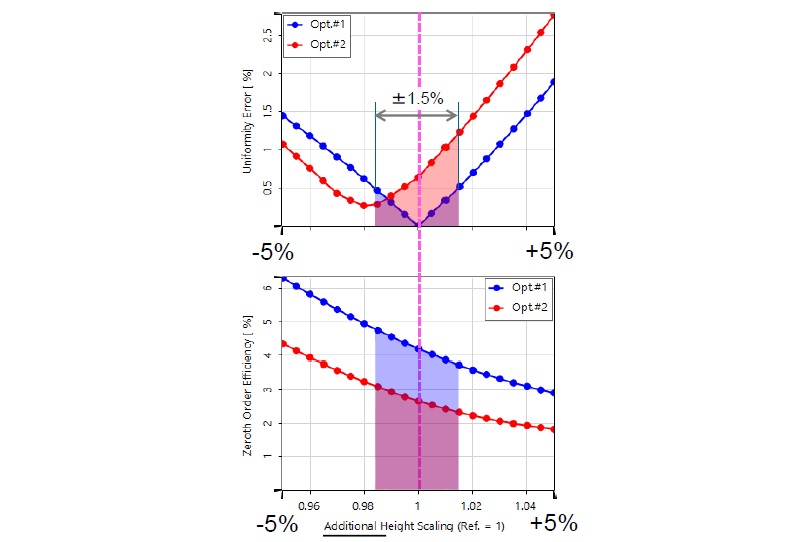
  • 製造時の高さの公差が±5 の範囲にある場合、品質関数がどのように振る舞うかを調査しました。
  • エッチング深さ誤差約±1.5% の許容範囲内のほとんどの部分（青と赤の部分の長さ）において、2 回目の最適化による設計は明らかに悪い均一性を示しています。
  • 一見すると、最適化#2 の最小均一性誤差（赤い曲線@ 0%）が中心でないのが不思議に思えるかもしれません。これは、#2 の最適化では0 次効率が低いことを優先し、そのために均一性をある程度犠牲にしたことが理由です。
  • その結果、2 番目の最適化の構造は、公差解析の全ての予想範囲において、明瞭に0 次光が低くなっています。

メモ
公差シミュレーション結果の基準値1 は、必ず調べた構造の個別に最適化された高さ（紫色の線で表示）を参照します。

公差シミュレーションの結論

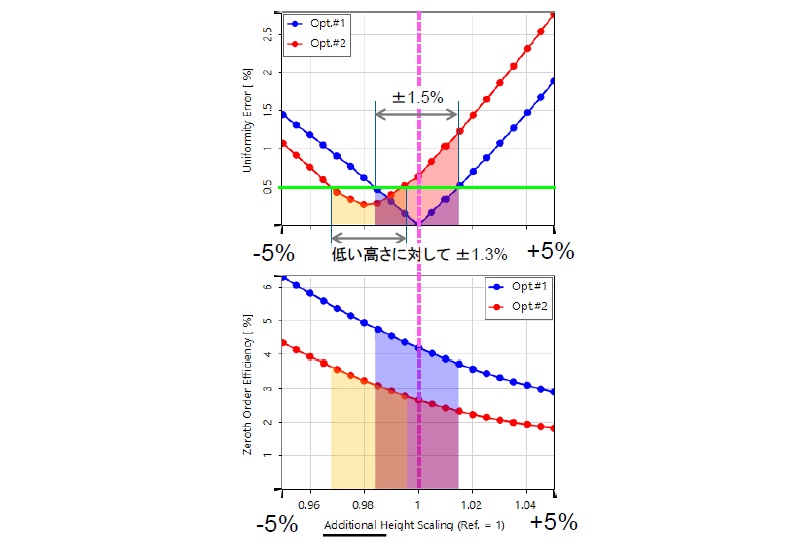
  • 公差テストにより、目的の用途に最も適した構造を決定するための、より良い情報基盤を得ることができます。
  • 2回目の最適化では、均一性誤差が最も小さい高さを使用した場合、±1.3% の公差範囲（黄色の部分の長さ）において、0.5% より小さい均一性誤差（緑の線）を得られることがわかります。
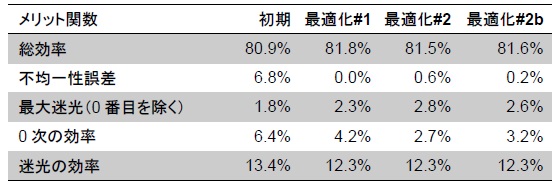
  • したがって、追加高さのスケーリング0 9825 707 7 nm) の2 番目の最適化結果は、全体的に適切な性能を持つ良い解決策となる可能性があります。以下の表では、「最適化 2 b 」という名称の最後の列に、その結果を示しています。

ドキュメント情報

タイトル ユーザー定義メリット関数による高NA ビームスプリッターの最適化
文書コード DOE.0005
文書バージョン 1.0
使用エディション VirtualLab Fusion Advanced
ソフトウェアバージョン 2021.1(Build 1.180)
カテゴリー Application Use Case
参考資料 Programmable Grating Analyzer
Design and Rigorous Analysis of Non Paraxial Diffractive Beam Splitter
Design of Diffractive Beam Splitters for Generating a 2D Light Mark

ファイルをダウンロード

関連する内容